Neste artigo vamos falar sobre o R² de uma forma simples e fácil.
O R² é uma medida de correlação que, além de fácil de calcular é intuitiva de interpretar. A maioria de nós já está familiarizada com a correlação e a métrica padrão dela. É simples: os valores de correlação que estão próximos de 1 positivo ou 1 negativo são bons.
Então, podemos analisar duas variáveis quantitativas, o peso o tamanho, por exemplo. Elas costumam ser fortemente relacionadas. Mas se o valor da correlação é próximo de zero, então a correlação é fraca.
E alguém pode se perguntar: “Porque é que devemos nos preocupar com o R² se já temos o R?” Ok, alguém pode pensar que o R² é muito semelhante ao seu “primo” mais moderno. Mas no R² a interpretação é mais fácil. Por exemplo, não é óbvio que quando R é igual a 0,7 é uma correlação duas vezes melhor do que quando R é igual a 0,5. No entanto, se o R² = 0,7, ele é 1,4 vezes melhor que R² = 0,5.
A outra coisa muito legal no R² é que é fácil e intuitivo de calcular. Vamos começar com um exemplo.
No gráfico estão plotados dados sobre Ratos. No eixo Y temos os pesos dos ratos. E no eixo X estão os números de identificação dos ratos de 1 a 7.
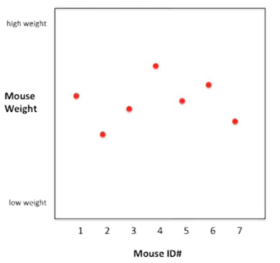
Podemos calcular a média dos pesos dos ratos e plotar essa média como uma linha que abrange o gráfico. E podemos calcular a variação dos dados em torno desta média como a soma do quadrado das diferenças entre o peso de cada Rato i e a média. Cada rato i é individualmente representado por um ponto vermelho. Já a média da diferença entre cada ponto e a média é elevada ao quadrado para que os pontos abaixo a média não cancele os valores dos pontos acima da média.
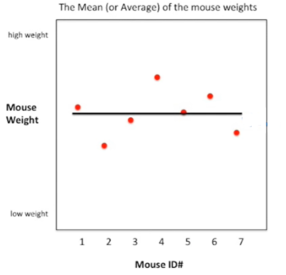
Agora, e se em vez de ordenar os nossos ratos pelo seu número de identificação nós os ordenássemos pelo seu tamanho, em vez de usar o número de identificação no eixo X, teremos o tamanho do menor rato como primeiro dado, no lado esquerdo e o maior rato como último dado, no lado direito. Então tudo o que fizemos foi reordenar os dados no eixo X. A média e a variação são exatamente as mesmas de antes.
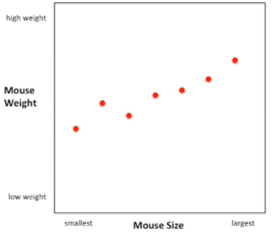
E daí podemos perguntar se, sabendo o peso médio dos ratos, essa é a melhor maneira de prever o peso individual de um rato i? Bom, a resposta é não, podemos fazer muito melhor!! Vamos ajustar uma linha aos dados.
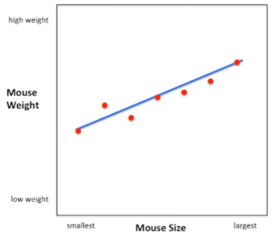
E ajustando essa linha, podemos prever o peso com ela. Se você me diz que tem um rato grande, eu posso olhar para minha linha e fazer uma boa estimativa sobre o peso dele.
Outra pergunta é se a linha azul que acabamos de desenhar se ajusta melhor aos dados do que a média. E se sim, quanto melhor?
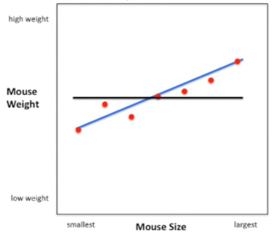
Só olhando, parece que a linha azul se ajusta melhor aos dados do que a média. Mas como quantificamos essa diferença r-quadrado? Abaixo está escrita a equação de R². Então vamos percorrê-la passo a passo.
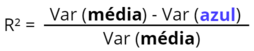
A primeira parte da equação, a Var(média), é apenas a variação em torno da média que já foi calculada. É a soma das diferenças quadradas entre os valores dados e a média. A segunda parte da equação, Var(azul), é a variação em torno da nossa nova linha azul. E isto é calculado de uma forma muito semelhante da forma anterior. Na Var(azul) queremos apenas a soma dos quadrados das diferenças entre os pontos de dados reais e nossa nova linha azul.
O numerador, que é a diferença entre a variação em torno da média e a variação em torno da linha azul. E esse resultado é então dividido pela variação em torno da média. Isso faz com que nosso R² esteja entre os valores zero e 1, porque a variação em torno da linha azul nunca será maior que a variação em torno da média, e nunca será menor que zero.
Agora vamos passar por um exemplo onde calculamos as coisas um passo de cada vez. Primeiro vamos começar com a variação em torno da média, que, fazendo os cálculos, será igual a 32, e a variação em torno da linha azul que, calculada, será 6. O que quer dizer que os dados da linha azul ajustam melhor os pontos que a média.
Uma vez que calculamos a variação em torno da média e a variação em torno de nossa linha azul, podemos inserir esses valores em nossa fórmula para R². E fazendo isso, obtemos que R² = 0,81 ou 81%. Isso significa que há 81% menos variação em torno da linha azul do que a linha média. Em outras palavras a relação entre tamanho e peso é responsável por 81% da variação total. Isso significa que a maior parte da variação nos dados é explicada pela relação “tamanho x peso”.
Agora, outro exemplo. Vamos comparar duas variáveis que talvez não sejam correlacionadas. No eixo Y, temos novamente o peso dos ratos. Mas agora, no eixo X, temos o tempo gasto em que o rato cheira um objeto.
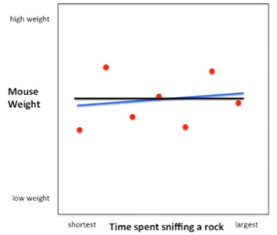
Quando calculamos a variâncias, obtemos que Var(média) = 32 e a Var(azul) = 30. Agora, vamos inserir esses valores em nossa fórmula para R² e fazendo as contas chegamos ao resultado R² = 0,06 ou 6%. Portanto, há apenas 6% menos variação ao redor da linha do que a média. Em outras palavras, a relação de “peso x tempo” representa apenas 6% da variação total, o que significa que quase nenhuma variação nos dados é explicada pela relação “peso x tempo”.
Quando alguém diz que este R² tem uma significância estatística de 0,9, você pode pensar que a relação entre essas duas variáveis é muito boa, pois aparentemente, a relação explicaria 90% da variação dos dados. Por outro lado, se dizem que R² tem uma significância de 0,01 o pensamento é de que ela não explica muita coisa e deve ter outra coisa que explique os 99% da variação restantes.
E quanto ao “velho e simples” R? Como é que R se relaciona ao R²? Bom, o valor de R² é simplesmente o valor de R elevado ao quadrado. Mas quando alguém diz que o R tem uma significância estatística de 0,9, jogamos isso para o R², quer dizer que 0,9×0,9=0,81. Significa que o R² explica 81% da variação dos dados.
E quando é dito que R tem significância de 0,5, então o R² tem 0,25 ou 25% de significância. O que pode ser ruim, se pensamos que ainda há que explicar os 75% restantes
Talvez os pesquisadores prefiram o R² ao R, pois ele é mais fácil e intuitivo para se fazer interpretações. Por exemplo: Qual é melhor? Um R = 0,7 ou um R = 0,5? Se convertermos para R², vemos que se esses valores forem convertidos para o R², temos que comparar os valores de R² = 0,49 ou 49% com o valor R² = 0,25.
E daí vemos que o primeiro valor é uma correlação melhor que a segunda e explica melhor as variações daqueles dados.
Outra coisa a mencionar é que o R² não indica a direção da correlação, porque os números ao quadrado nunca são negativos. Se a direção da correlação não for óbvia, você pode dizer que as duas variáveis positiva ou negativamente correlacionadas com R quadrado igual a … (blá blá blá e tudo o que já foi explicado acima). E qualquer que seja esse valor, essas são as duas ideias principais para R²: ele é a porcentagem de variação explicada pela relação entre duas variáveis.
E também se alguém lhe der um valor para o velho R, então você entenderá o que está acontecendo.
Esse artigo foi retirado da página StatQuest. Você pode ver o vídeo clicando Aqui