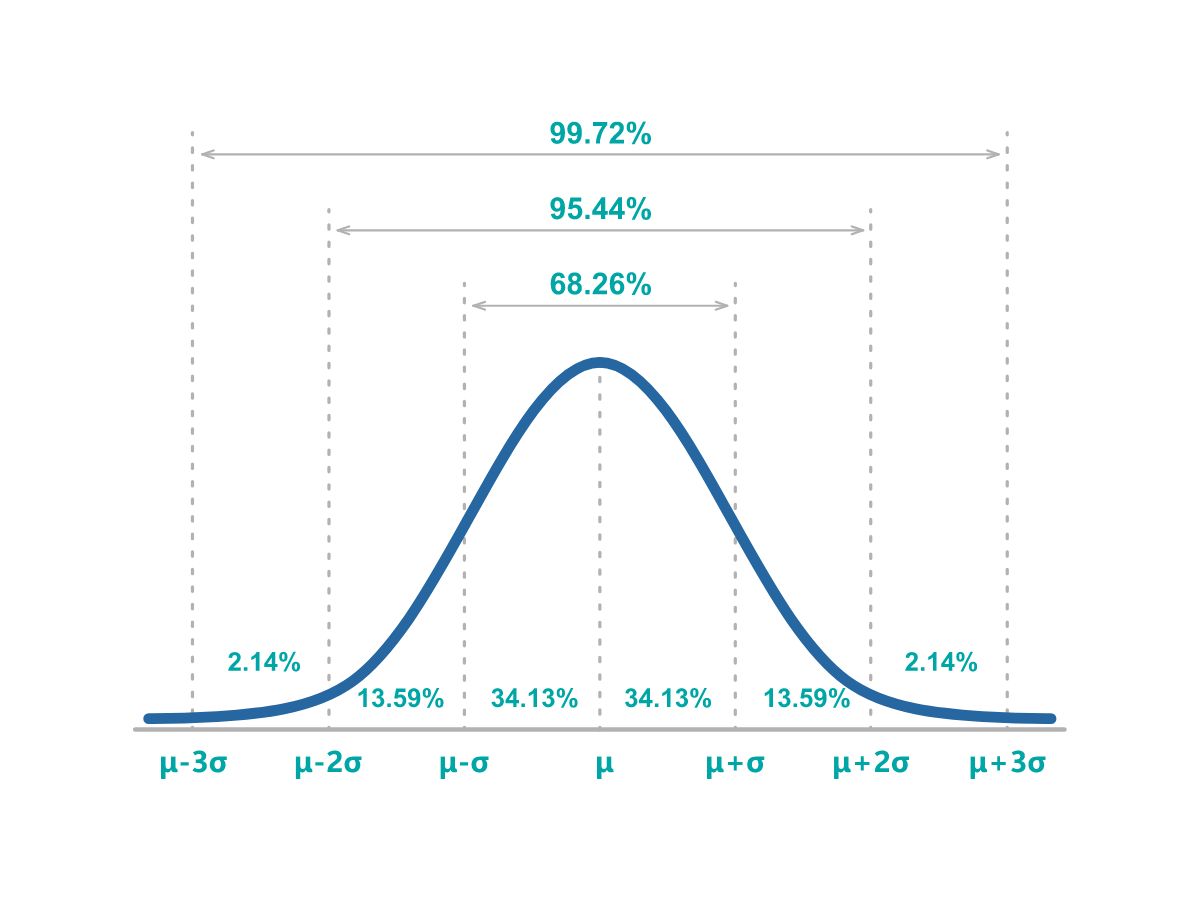
A distribuição normal é um conceito super importante na estatística e aqui vamos falar sobre o básico. Você pode ouvir falar sobre “normais” ou “Gaussianas”, ou até a “curva de sino”. São todos nomes para a mesma curva.
Neste exemplo abaixo, esta curva representa a altura das pessoas. As pessoas podem ser baixas ou médias ou altas… ou algo entre isso.
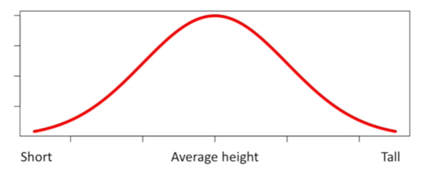
O eixo Y representa a probabilidade relativa de observar alguém muito baixo, muito alto ou médio. Por exemplo, é relativamente raro ver uma pessoa muito baixa. Portanto, a altura da curva do sino neste ponto é relativamente baixa. Por outro lado, é bastante comum ver alguém próximo da estatura média. Portanto, o gráfico de sino nesta área é muito alto. E é relativamente raro ver uma pessoa muito alta. Portanto, a curva de sino também é relativamente baixa nesta área.
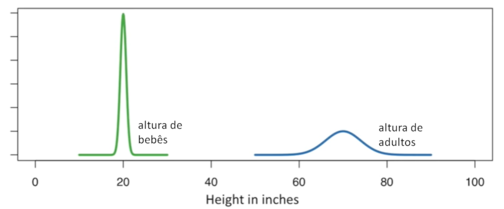
Estas são duas distribuições normais. A verde é referente às alturas de bebês do sexo masculino e a curva azul é referente às alturas de homens adultos. A altura média de um bebê é de 20 polegadas. A altura média dos adultos é de 70 polegadas. A distribuição normal está sempre centrada na média. Olhando para este gráfico, podemos dizer que há uma alta probabilidade de que um bebê tenha entre 21 e 22 centímetros de altura. Os adultos, por outro lado, são mais propensos a ter entre 69 e 71 polegadas de altura.
Como você deve ter notado, a curva de um bebê é muito maior que a curva de um adulto. Isso acontece porque os adultos têm uma gama maior de possibilidades do que os bebês. Quanto mais opções você tiver para algo, menor a probabilidade de sua medida ser uma delas.
A área da curva é definida pelo seu desvio padrão. Observando a curva, podemos dizer que a altura do bebê tem um desvio padrão relativamente pequeno em relação ao adulto. O desvio padrão da altura do bebê é 0,6 polegadas. E o desvio padrão da altura adulta é 4 polegadas. Saber o desvio padrão é importante porque a curva normal é desenhada de modo que 95% das medições fiquem entre ± 2 desvios padrão em torno da média. Isso significa que 95% das medidas de altura do bebê estão dentro de 20 ± 1,2 polegadas. E isso significa que 95% das medidas de altura de adultos caem dentro de 70 ± 8 polegadas.
Para traçar uma distribuição normal, você precisa saber as duas coisas a seguir: Primeiro, a média das medidas, valor que informa onde está o centro da curva. Em segundo lugar, o desvio padrão das medidas, que informa a largura da curva. E sua largura determina quão alta será a curva, pois quanto mais larga a curva, menor a altura, e quanto mais estreita a curva, maior a altura.
A curva então nos diz que é mais provável que a altura do bebê esteja dentro de ±1,2 polegadas da média. E isso nos diz que é menos provável que a altura de um adulto esteja dentro de ±8 polegadas da média. Muitos deles seguem uma distribuição normal.
Nós falamos sobre alturas aqui, mas além disso variáveis como peso, tempo de deslocamento e quantidades também seguem a distribuição Normal. A distribuição normal é uma espécie de mágica, pois você pode vê-la muito na natureza. Mas há uma razão para isso. E é por isso que é muito útil para estatísticas também. Haverá mais posts falando sobre isso, inclusive sobre o Teorema do Limite central.
Esse artigo foi retirado do vídeo do StatQuest. Você pode acessá-lo clicando Aqui